LIMIT DAN TURUNAN/DIFFERENSIAL MATERI KELAS XII
Turunan fungsi (diferensial) adalah fungsi lain dari suatu fungsi sebelumnya, misalnya fungsi f menjadi f’ yang mempunyai nilai tidak beraturan. Konsep turunan sebagai bagian utama dari kalkulus dipikirkan pada saat yang bersamaan oleh Sir Isaac Newton (1642 – 1727). Turunan (diferensial) digunakan sebagai suatu alat untuk menyelesaikan berbagai masalah dalam geometri dan mekanika.
Aturan menentukan turunan fungsi
Turunan dapat ditentukan tanpa proses limit. Untuk keperluan ini dirancang teorema tentang turunan dasar, turunan dari operasi aljabar pada dua fungsi, aturan rantai untuk turunan fungsi komposisi, dan turunan fungsi invers.
Turunan dasar
Aturan – aturan dalam turunan fungsi adalah :
- f(x), maka f'(x) = 0
- Jika f(x) = x, maka f’(x) = 1
- Aturan pangkat : Jika f(x) = xn, maka f’(x) = n X n – 1
- Aturan kelipatan konstanta : (kf) (x) = k. f’(x)
- Aturan rantai : ( f o g ) (x) = f’ (g (x)). g’(x))
Turunan jumlah, selisih, hasil kali dan hasil bagi kedua fungsi
Misalkan fungsi f dan g terdiferensialkan pada selang I, maka fungsi f + g, f – g, fg, f/g, ( g (x) ≠ 0 pada I ) terdiferensialkan pada I dengan aturan :
- ( f + g )’ (x) = f’ (x) + g’ (x)
- ( f – g )’ (x) = f’ (x) – g’ (x)
- (fg)’ (x) = f’(x) g(x) + g’(x) f(x)
- ((f)/g )’ (x) = (g(x) f’ (x)- f(x) g’ (x))/((g(x)2)
Turunan fungsi trigonometri
- d/dx ( sin x ) = cos x
- d/dx ( cos x ) = – sin x
- d/dx ( tan x ) = sec2 x
- d/dx ( cot x ) = – csc2 x
- d/dx ( sec x ) = sec x tan x
- d/dx ( csc x ) = -csc x cot x
Turunan fungsi invers
(f-1)(y) = 1/(f’ (x)), atau dy/dx 1/(dx/dy)
Contoh soal :
- .Diketahui f’(x) adalah turunan dari f(x) = 5x3 + 2x2 + 6x + 12,tentukan nilai f’(x) adalah….
Penyelesaian :
f(x) = 5x3 +2x2 + 6x + 12
f’(x) = 15x2+ 4x +6
f’(3) = 15 . 32 +4 . 3 + 6
= 135 + 12 + 6
= 153
- Turunan pertama dari f(x) = sin3(3x2 – 2) adalah f‘(x) = …
Penyelesaian:
f(x) = sin3(3x2 – 2)
f’(x) = sin(3-1)(3x2 – 2).3.6x.cos (3x2 – 2)
= 18x sin2(3x2 – 2) cos (3x2 – 2)
1. Turunan pertama dari fungsi f(x) = (2-6x)³ adalah?
Penyelesaian:
Fungsi pada soal berbentuk fungsi lain yang eksponensial. Untuk menentukan turunannya, digunakanlah aturan rantai.
Jika f(x) = (u(x))ⁿ maka f ‘ (x) = n.(u(x))ⁿ-1 . (u ‘ (x))
Perhatikan pembahasannya pada gambar di bawah ini.
f ‘ (x) = -18(4-24x+36x²)
2. Turunan pertama dari fungsi trigonometri f(x) = 5sinxcosx adalah?
Penyelesaian:
- Fungsi diatas berbentuk fungsi perkalian jadi untuk menentukan turunannya, digunakanlah aturan perkalian.
Jika f(x) = u(x).v(x)
Maka f ‘ (x) = u ‘ (x). v(x) + u(x).v ‘ (x)
- Untuk fungsi trigonometri, turunan sinx adalah cosx dan turunan cosx adalah -sinx.
Lebih lengkapnya, perhatikan gambar di bawah ini.
Jadi turunan f(x) 5sinxcosx adalah f ‘ (x) = 5(cos²x – sin²x)
atau f ‘ (x) = 5cos2x
3. Diketahui biaya produksi barang sebuah perusahaan dinyatakan dalam fungsi f(x) = 8x² – 120x. Kemudian harga jual tiap barang dinyatakan dalam f(x) = 1/3 x² – 10x + 200. x menyatakan jumlah barang. Maka, untuk mencapai keuntungan maksimum, jumlah barang yang harus diproduksi adalah sebanyak…
Penyelesaian:
Biaya Produksi = 8x² – 120x
Harga Jual tiap barang = 1/3 x² – 10x + 200
Keuntungan = Harga Jual semua Barang – Biaya Produksi
= (Jumlah Barang dikali Harga Jual tiap Barang) – Biaya Produksi
= x.(1/3 x² – 10x + 200) – (8x² – 120x)
= (1/3 x³ – 10x² + 200x) – (8x² – 120x)
= 1/3 x³ – 18x² + 320x
Untuk mencapai keuntungan maksimum, maka nilai stationernya = 0
f ‘ (x) = 0
x² -36x + 320 = 0
(x -16)(x – 20) = 0
x = 16 atau x = 20.
Jadi, jumlah barang yang harus dijual adalah 16 atau 20 buah.
4. Biaya proyek sebuah perusahaan per harinya dinyatakan oleh fungsi f(x) = 3x + 1200/x – 60 (dalam juta rupiah). Tentukan total biaya produksi selama x hari agar diperoleh biaya minimum?
Penyelesaian:
Biaya Proyek per hari = 3x + 1200/x – 60
Biaya Proyek per x hari = (3x + 1200/x – 60)/x
= 3 + 1200/x² – 60/x
= 3x² – 60x + 1200
Agar biaya minimum, maka nilai stationer = 0 atau f ‘ (x) = 0.
f ‘ (x) = 0
6x – 60 = 0
6x = 60
x = 10 hari.
Biaya minimum per hari
= 3x + 1200/x – 60
= 3(10) + 1200/10 -60
= 30 + 120 – 60
= 90 juta rupiah
Maka total biaya minimum proyek selama 10 hari adalah
= 90 juta rupiah x 10 hari
= 900 juta rupiah.
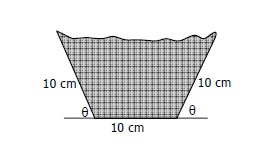
5. Sebuah talang air akan dibuat dari lembaran seng yang lebarnya 30 cm dengan melipat lebarnya atas menjadi 3 bagian yang sama, seperti terlihat pada gambar. Jika θ menyatakan besar sudut dnding talang dengan bidang alasnya, maka volume air yang tertampung paling banyak bila θ …
Lipatan seng berbentuk trapesium.
Untuk mencapai volume air maksimum, maka nilai stationer dari luas trapesium = 0.
Pembahasannya ada pada gambar di bawah ini.
*Semoga Bermanfaat*
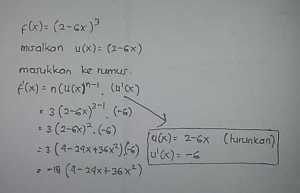
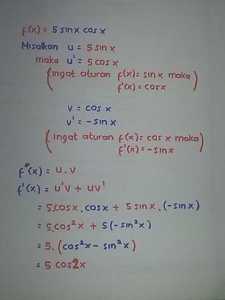



Komentar
Posting Komentar